الدقة (Accuracy) ليست كل شيء!

خلال عملك او تعلمك لبناء نماذج تعلم الاله مررت بمقاييس مختلفة لقياس أداء نماذج تعلم الالة, وربما كان التركيز على Accuracy, بحكم انه من المقاييس الرئيسية تقريبًا في جميع القياسات والاثباتات. لكن ماذا لو اردت تحسين هذا النموذج؟ او اردت اختبار سرعته وجاهزيته؟ ماذا لو كان غير قادر مستقبلا على التكيف مع تنوع واختلاف البيانات.

لنفرض ان مجموعة البيانات لديك غير متوازنة! فمثلا لديك 100 صورة لسيارة و 20 صورة لطائرة وعند تدريبك للنموذج اعطاك نتيجة 90% كدقة! لكن في الحقيقة هو استطاع ان يميز العينة ذات العدد الأكبر بنجاح وربما فشل في تحديد الطائرات!

حتى نفهم هذه المشكلة الخاصة بـAccuracy يجب علينا ان نلقي نظرة تفصيلية على مصفوفة الارتباك او جدول الاحتمالات أو مصفوفة الخطأ Confusion Matrix.

ما هو Confusion Matrix ؟

مصفوفة الارتباك هي مصفوفة تلخص أداء نموذج التعلم الآلي على مجموعة من بيانات الاختبار. يستخدم لقياس أداء نماذج التصنيف ، والتي تهدف إلى توقع كل تصنيف لكل حالة مدخلة. تعرض المصفوفة عدد الإيجابيات الحقيقية (TP) ، السلبيات الحقيقية (TN) ، الإيجابيات الزائفة (FP) ، السلبيات الزائفة (FN) التي ينتجها النموذج في بيانات الاختبار.

تخيل انك تبني نموذج ألة يقوم بتمييز البريد الالكتروني اذا كان “رسائل إلكترونية مزعجة” او “رسائل إلكترونية غير مزعجة”, جدول الارتباك او مصفوفة الخطأ تعطي لمحة على أداء نموذج الالة وكيف يستطيع التنبؤ او تمييز هذه الرسائل.

يكون شكل مصفوفة الارتباك كما في الجدول التالي:

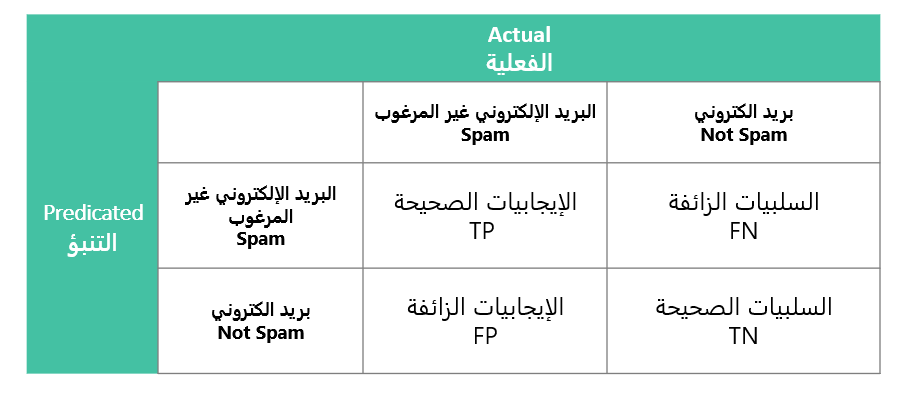
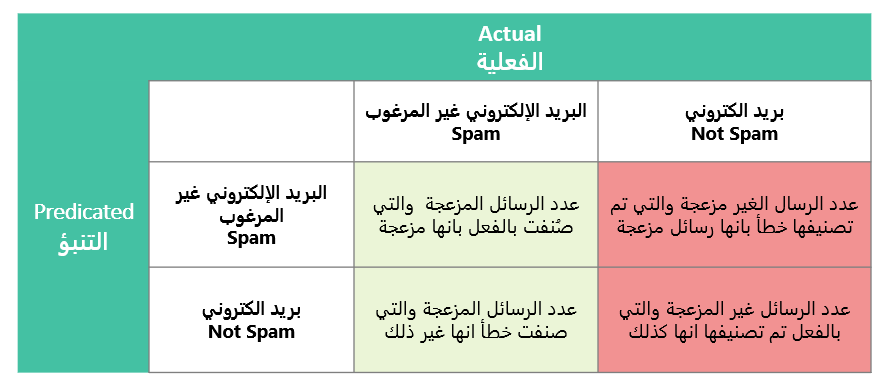
توضيح الجدول باستخدام مثال تصنيف رسائل البريد الالكتروني

1. الإيجابيات الصحيحة (TP – True Positives):
   • توقع صحيح.
   عدد الحالات التي تم توقعها بشكل صحيح على أنها موجبة بواسطة النموذج. بعبارة أخرى ، هذه هي الحالات التي توقع فيها النموذج نتيجة إيجابية ، وكانت النتيجة الفعلية إيجابية بالفعل. في مثالنا هذه هي الحالات التي تم التنبؤ بأنها رسائل إلكترونية مزعجة (Spam) وكانت النتيجة الفعلية هي رسائل إلكترونية مزعجة (Spam) .
2. السلبيات الصحيحة (TN – True Negatives):
   • توقع صحيح.
   عدد المثيلات التي تم توقعها بشكل صحيح على أنها سالبة بواسطة النموذج. هذه هي الحالات التي توقع فيها النموذج نتيجة سلبية ، وكانت النتيجة الفعلية سلبية بالفعل في مثال البريد الالكتروني هي عدد رسائل البريد الإلكتروني التي ليست رسائل غير مرغوب فيها في الواقع (Not Spam) ، وقد توقعها النموذج بشكل صحيح على أنها ليست رسائل غير مرغوب فيها (Not Spam).
3. الإيجابيات الزائفة (FP – False Positives):
   • توقع خاطئ.
   عدد الحالات التي تم توقعها بشكل غير صحيح على أنها موجبة بواسطة النموذج. هذه هي الحالات التي توقع فيها النموذج نتيجة إيجابية ، لكن النتيجة الفعلية كانت سلبية عدد رسائل البريد الإلكتروني التي ليست بريدًا عشوائيًا في الحقيقة (Not Spam) ، لكن النموذج أخطأ في توقعها على أنها بريد عشوائي (Spam) .
4. السلبيات الزائفة (FN – False Negatives):
   • توقع خاطئ.
   عدد الحالات التي تم توقعها بشكل غير صحيح على أنها سلبية بواسطة النموذج. هذه هي الحالات التي توقع فيها النموذج نتيجة سلبية ، لكن النتيجة الفعلية كانت إيجابية. عدد رسائل البريد الإلكتروني غير المرغوب فيها في الواقع (Spam) ، لكن النموذج أخطأ في توقعها على أنها ليست بريدًا (Not Spam) .

1. الدقة – Accuracy

يوفر مقياسًا شاملاً لصحة النموذج, نسبة الحالات المصنفة بشكل صحيح (كل من الإيجابيات الحقيقية TP والسلبيات الحقيقية TN) من إجمالي الحالات في مجموعة البيانات. بعبارة أخرى مجموع ما تنبئ به النموذج بشكل صحيح مقسوما على مجموع البيانات.

الدقة = مجموع التنبؤات الصحيحة / مجموع التنبؤات.

وبما ان المثال هو تصنيف ثنائي (Binary Classification) فسيكون حساب الدقة بالمعادلة التالية

Accuracy = (TP + TN) / (TP + TN + FP + FN)

2. معدل الخطأ (Error Rate)

معدل الخطأ هو نسبة عدد الأمثلة المصنفة بشكل غير صحيح (الإيجابيات الزائفة FP والسلبيات الزائفة FN) إلى إجمالي عدد الأمثلة في مجموعة البيانات. يقدم هذا المقياس لمحة عامة عن كمية الأمثلة التي تم تصنيفها بشكل غير صحيح بواسطة النموذج. على العكس من الدقة، يركز معدل الخطأ على الأمثلة التي تم التنبؤ بها بشكل غير صحيح بغض النظر عن إيجابيها أو سلبيتها.

Error Rate = (FP + FN) / (TP + TN + FP + FN)

او باختصار

الخطأ = 1 – الدقة

3. معدل الإيجابيات الصحيحة – Recall

يسمى أيضا (Sensitivity) نسبة الإيجابيات الصحيحة (TP) إلى مجموع الإيجابيات الصحيحة (FP) والسلبيات الزائفة (TN) . يقيس قدرة النموذج على التعرف بشكل صحيح على الحالات الإيجابية من بين الحالات الفعلية الإيجابية في مجموعة البيانات.

Recall = True Positives / (True Positives + False Negatives)

• الإيجابيات الحقيقية (TP): عدد الحالات التي تم توقعها بشكل صحيح على أنها موجبة (بريد عشوائي Spam) بواسطة النموذج.
• السلبيات الكاذبة (FN): عدد الحالات التي تم توقعها بشكل غير صحيح الرسال الغير مزعجة والتي تم تصنيفها خطأ بانها رسائل مزعجة.

4. القيمة التنبؤية الإيجابية – Precision

يمثل نسبة الحالات الإيجابية التي تم التنبؤ بها بشكل صحيح من بين جميع الحالات التي تم توقعها على انها إيجابية بواسطة النموذج. . بمعنى آخر ، يقيس دقة التنبؤات الإيجابية للنموذج. تشير الدقة العالية إلى أنه عندما يتنبأ النموذج بشيء ما على أنه إيجابي (بريد عشوائي) ، فمن المحتمل أن يكون صحيحًا.

Precision = TP / (TP + FP)

• الإيجابيات الحقيقية (TP): عدد الحالات التي تم توقعها بشكل صحيح على أنها موجبة (بريد عشوائي) بواسطة النموذج.
• الإيجابيات الكاذبة (FP): عدد الحالات التي تم توقعها بشكل غير صحيح على أنها موجبة (بريد عشوائي) بواسطة النموذج.

ما لمشكلة في مجرد اعتمادنا على Accuracy!

لنفترض أن لدينا مجموعة بيانات بريد إلكتروني حيث 95٪ من رسائل البريد الإلكتروني ليست رسائل غير مرغوب فيها (شرعية) و 5٪ فقط من رسائل البريد الإلكتروني هي في الواقع رسائل غير مرغوب فيها. في مجموعة البيانات غير المتوازنة هذه ، يوجد عدد قليل جدًا من رسائل البريد الإلكتروني العشوائية مقارنة بالعدد الإجمالي لرسائل البريد الإلكتروني.

الآن ، تخيل انك قمت ببناء نموذج آلة يصنف جميع رسائل البريد الإلكتروني على أنها ليست بريدًا عشوائيًا. نظرًا للطبيعة غير المتوازنة لمجموعة البيانات ، سيحقق نموذج تصفية البريد العشوائي هذا دقة عالية لأنه يصنف بشكل صحيح الغالبية العظمى من رسائل البريد الإلكتروني ، والتي ليست بريدًا عشوائيًا. قد تصل الدقة إلى حوالي 95٪ ، مما يشير إلى أنه تحصٌل على جميع رسائل البريد الإلكتروني غير العشوائية بشكل صحيح تقريبًا.

ومع ذلك ، نظرًا لأن نموذج تعلم الآلة الذي تم بنائه لتصفية البريد العشوائي لا يتوقع أبدًا أي بريد إلكتروني غير مرغوب فيه ، فإن استدعائه لفئة البريد العشوائي سيكون 0. وهذا يعني أنه يفشل في تحديد أي من رسائل البريد الإلكتروني العشوائية الفعلية, على الرغم من أنه يعمل بشكل جيد مع غالبية رسائل البريد الإلكتروني غير العشوائية. وهذا يعني ان مقياس Recal في الحقيقة يعطي نتيجة صفر!, وهذا بالتأكيد يخبرك ان نموذج الالة الذي يصنف البريد الإلكتروني لا يهمل بالشكل المطلوب ، وأيضا يخبرك ان Acuracy ليس كل شيء!.

الان, على نفس هذا السيناريو سنفرض ان Recall لديك يساوي 1, وحصل على هذه النتيجة لأنه فادر على تصنيف جميع رسائل البريد الإلكتروني العشوائية الفعلية بشكل صحيح. بحيث يتم الكشف عن كل بريد إلكتروني عشوائي ، ولا توجد سلبيات خاطئة في هذه الحالة.

ومع ذلك ، يصنف المرشح أيضًا بشكل غير صحيح العديد من رسائل البريد الإلكتروني الشرعية كرسائل غير مرغوب فيها. هذا من شأنه أن يؤدي إلى (القيمة التنبؤية الإيجابية – Precision) منخفض. نظرًا لأن الدقة هي نسبة التنبؤات الإيجابية الحقيقية بين جميع التوقعات الإيجابية ، وفي هذه الحالة ، تكون جميع التوقعات إيجابية (بريد عشوائي) ، ولكن العديد منها عبارة عن إيجابيات خاطئة (رسائل بريد إلكتروني شرعية مصنفة بشكل خاطئ على أنها بريد عشوائي) ، فإن Precision سيكون منخفض للغاية.

لذلك ، في حين أن Recall مثالي (1.0) بحيث انه يتم اكتشاف جميع رسائل البريد الإلكتروني العشوائية الفعلية ، فإن Precision منخفض لأن غالبية التوقعات الإيجابية (تنبؤات البريد العشوائي) غير صحيحة. يوجد هنا مفاضلة بين Precision وRecall وكيف يمكن أن يؤثر تحسين أحدهما سلبًا على الآخر. لكن كيف نستطيع الموازنة بين المقياسين؟

F1-Score

F1-Score هي مقياس تقييم يأخذ في الاعتبار Recall وPrecision ، مما يجعله مفيدًا بشكل خاص عند التعامل مع مجموعات البيانات غير المتوازنة مثل هذا السناريو الذي نتعامل معه أو المواقف التي نريد فيها الموازنة بين هذين المقياسين.

F1 = 2 * (precision * recall) / (precision + recall)

في F1-Score يتم توزيع الوزن بالتساوي بين Precision وRecall, ولكن اذا اردنا تخصيص التوزيع لكل مقياس وزن خاص فيمكن استخدام ب F_\beta “اف بيتا”. بحيث يكون لكل مقياس توزيع خاص به. بحيث \beta هو المتحكم في التوازن بين Precision وRecall, قيمة بيتا الافتراضية هي 1.0 ، وهي نفس قيمة مقياس F. اذا قمنا بإعطاء بيتا قيمة قليلة ، مثل 0.5 ، هنا جعلنا للـPrecision وزنًا اكبر وبالعكس للـRecall، بينما اذا اسندنا قيمة كبيرة لbeta ، مثل 2.0 ، جعلنا وزن Recall اكبر من Precision. بمعنى أخر عندما تكون beta > 1 ، تضع درجة F_β مزيدًا من التركيز على precision، مما يجعل النموذج يعطي الأولوية لتقليل الإيجابيات الزائفة. عندما تكون beta<1 ، تؤكد الدرجة F_β على recall، مما يجعل النموذج يركز على تقليل السلبيات الكاذبة. يعتبر مقياس مفيد لاستخدامه عندما يكون كل من Precision وRecall مهمين ولكن هناك حاجة إلى مزيد من الانتباه قليلاً على أحدهما أو الآخر ، مثل عندما تكون السلبيات الخاطئة أكثر أهمية من الإيجابيات الخاطئة أو العكس.

الخلاصة

في الختام، تُوجز هذه المفاهيم المعقدة والمهمة في مجال تقييم نماذج التعلم الآلي بمفهوم بسيط: مصفوفة الارتباك. إن فهم العناصر المختلفة في هذه المصفوفة والمقاييس المرتبطة بها يمكن أن يساعد في تحسين الأداء وتعزيز دقة النماذج. وعلى الرغم من أن الدقة لها مكانتها، فإن الانتباه لتوازن بين مقاييس Recall وPrecision يمكن أن يكون حلاً ذكيًا في حالات مجموعات البيانات غير المتوازنة. عندما نستخدم الأدوات المناسبة مثل F1-Score و F_\beta، يمكننا تحقيق توازن يحقق الهدف المطلوب بنجاح.

تذكر أن الهدف النهائي من هذه المقاييس هو تحسين أداء النماذج وجعلها أكثر فعالية في توقع وتصنيف البيانات. إذا تم تطبيق هذه المفاهيم بشكل صحيح، يمكن أن تكون لديك فهمًا أعمق لأداء النماذج وكيفية تحسينها بناءً على متطلبات مهمتك الخاصة.

بالتأكيد، هذه المصفوفة والمقاييس قد تبدو معقدة في البداية، ولكن مع الممارسة والتطبيق العملي، ستكتسب مهارات أفضل في تحليل وتقييم أداء نماذج التعلم الآلي بكل ثقة. فلا تتردد في تطبيق هذه المفاهيم في مشاريعك واستمر في تطوير فهمك ومهاراتك في هذا المجال المثير والمتطور باستمرار.

المصادر

A Gentle Introduction to the Fbeta-Measure for Machine Learning – MachineLearningMastery.com

Confusion Matrix Explained. Simple explanation with examples… | by Nathan Timothy Handoko | Towards Data Science

Is accuracy EVERYTHING?. Various metrics to evaluate the… | by Shubhankar Rawat | Towards Data Science