تأثير البيانات المفقودة على دقة الاستنتاج: أساليب تعويض البيانات المفقودة (2)

في عالم اصبح مليئ بالبيانات, لا تزال القيم المفقودة احد اكثر الاشياء قدرة على جعل اكثر التحليلات المحكمة تظهر في حالة من الفوضى. كعالم بيانات او باحث ستواجه الكثير من مجموعات البيانات التي تغيب فيها العديد من السجلات المهمة, تاركه فراغ في فهمنا للبيانات وايضًا ربما تعرض دقة استنتاجنا للخطر.

حتى لاتطيل ونعيد ماتكلمنا عنه سابقًا, في هذه التدوينة سنتعرف على العديد من تقنبات التي ستساعدنا على التعامل مع هذه السجلات المفقودة, تنقسم هذه التقنيات الى عدة اقسام وكل قسم يندرج تحته انواع مختلفه من طرق ملئ الفراغ بالقيم المناسبة. باذن الله ستصبح بعد هذه المقالة ملم بطرق حل البيانات وتكون منطلق لك في رحلة لاستخراج الحقائق.

سنتحدث هنا عن اكثر الطرق شيوعُا للتعامل مع البيانات المفقودة, لكن من المهم ان تعرف ان هذه الحلول تفترض ان نوع البيانات المفقودة هو ْ”MCAR”.

1. الحذف Deletion

هذا هو أبسط طريقة للتعامل مع البيانات المفقودة. تتضمن إزالة جميع البيانات التي تحتوي على قيم مفقودة. يمكن أن يكون هذا فعالًا إذا كانت البيانات المفقودة قليلة نسبيًا، ولكن يمكن أن يؤدي أيضًا إلى فقدان الكثير من البيانات.

1. تحليل الحالات الكاملة Complete-Case Analysis

في هذه الحالة والتي يطلق عليها أيضًا “Listwise deletion”, تعتمد هذه الطريقة على حذف الصف بشكل كامل اذا كان يحتوي على أي قيمة مفقودة, بمعنى أخر ناخذ لو قمت بعمل استبيان فانك فقط ستعتمد على المشاركين الذين قاموا بتعبئة الاستبيان كاملًا, ويمكن استخدام هذا النوع من المعالحة مع البيانات النصية والرقمية على حد سواء, الميزة الوحيدة من هذا العلاج هو ان تحليلك فقط قائم على البيانات الكاملة فقط, لكن هذه البيانات الكاملة وبسبب حذف القيم الناقصة ان صح التعبير, سبب نقص في عدد مجموعة البيانات وهذا بالطبع يقودنا الى فقذ قوة التحليل. واذا كانت هذه الطريقة تحتوي على ميزة فهي وللاسف مساؤها أكثر على سبيل المثال لا الحصر, ربما تصبح البيانات لديك متحيزة, اذا كانت هذه البيانات المفقودة ليست ظمن “بيانات مفقودة بشكل عشوائي تماما MCAR”. ومع هذه العيوب يكون هذا هو الخيار الافتراضي في جميع برامج الاحصاء وايضُا في المجال الطبي هذه الطريقة هي الاكثر شيوعُا.

titanic_complete_case = titanic_df.dropna()
create_visualization(titanic_complete_case, 'Complete-Case Analysis (Listwise Deletion)')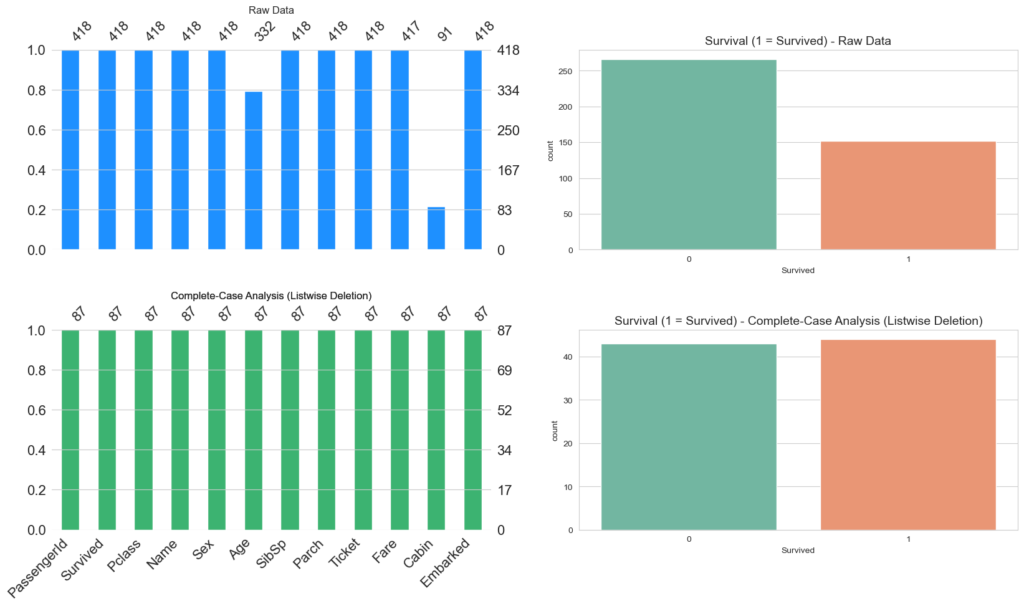

الصورة البيانية السابقة تتكون من صفين, الصف الاول يوضح شكل البيانات كماهي “الاصلية”, ولا يخفى عليك ان مجموعة البيانات التي نعمل عليها هي التايتانيك. Hello World dataset لعلوم البيانات, نلاحظ ان عدد العناصر لدينا 418, والمتغير المهم لدينا لنفترض انه النجاه, تلاحظ بعد حذف الصفوف التي تحتوي على اي قيمة فارغة تم التخلص من 80% البيانات تقريبا. هذا لا يجعل مجال للشك ان تحليلاتنا سوف تتاثر بعد التخلص من هذا الكم الهائل من العينات.

2. تحليل الحالات المتاحة Available-Case Analysis

يسمى ايضًا “Pairwise deletion”, هنا نقوم بمحاولة تقليل الفقد الذي حدث في Listwise. لفهم هذه الطريقة فكر بـمصفوفة الارتباط “Correlation Matrix”, الارتباط هو قياس لايجاد قوة العلاقة بين متغيرين. لكل زوج من المتغيرات التي تتوفر عنها بيانات, معامل الارتباط سياخذ هذه البيانات في الاعتبار. مايمز هذا النوع انه اذا كنا متاكدين ان البيانات MCAR سيكون لدينا نتائج غير متحيزه في مجموعة البيانات الكبيرة اما في المجموعات الصغيرة سيكون من الصعب حسابها.

مقارنةً بـListwise اذا كانت العلاقات بين المتغيرات منخفضة سيكون الاخير اكثر فعالية, وعلى النقيض اذا كانت العلاقات بين البيانات مرتفعة سيكون Listwise اكثر فعالية من Pairwiswe.

titanic_available_case = titanic_df.copy()
titanic_available_case = titanic_available_case.drop('Cabin',axis=1)
create_visualization(titanic_available_case, 'Available-Case Analysis (Pairwise Deletion)')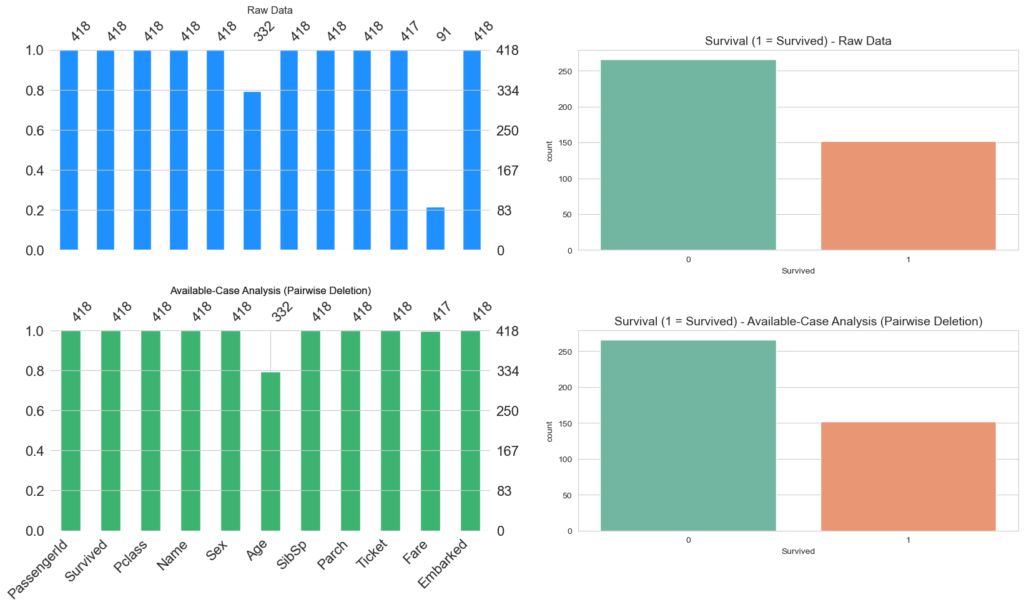

على النقيض من Listwise, هنا نتأكد هل فيه علاقات بين المتغيرات ونتخلص من المتغيرات التي لاتجدي نفع في تحليلاتنا. هنا تلاحظ نم نفقد اي عينه لكن خسرنا مٌتغير. بالطبع لايوجد شئ بدون نتائج عكسية, ستؤثر طريقة المعالجة هذه على التحليلات بشكل او باخر.

3. الاعتماد على تحليلك

بعض الاحيان تجد ان البيانات مفقودة بنسبة 60%, يمكن حذفها والاستغناء عنها اذا كانت لاتشكل اهمية الى عملية التحليل, الكلام السابق لايستند على اي شئ علمي وانما يتم قياسه اثناء عملية التحليل ولكل بيانات حالاتها الخاصة.

titanic_rely_on_analysis = titanic_df.dropna(thresh=len(titanic_df) * 0.90, axis=1)
create_visualization(titanic_rely_on_analysis, 'Relying on Your Analysis')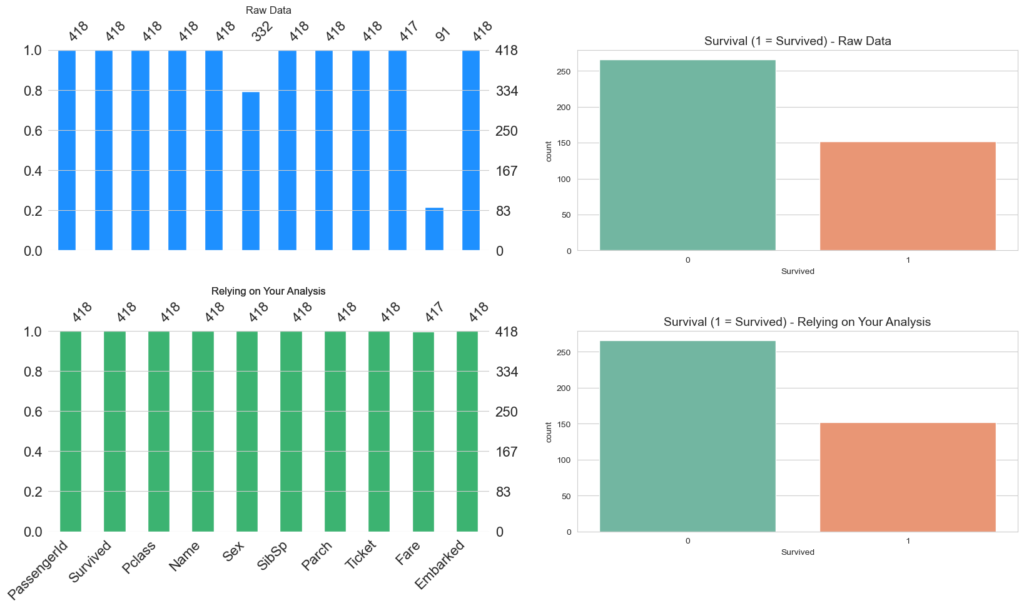

هنا حددت Threshold عند 0.95, و المحور على المتغيرات “الاعمدة”, سيتم الاخذ في الاعتبار الاعمدة المكتملة بنسة 95% فقط, تلاحظ اختلاف عدد الاعمدة بين الصور البيانية.

2. التعويض Imputation

في علوم البيانات والإحصاء، التعويض (أو الإكمال) هو عملية ملء القيم المفقودة في مجموعة البيانات بقيم مقدرة أو مستندة إلى قيم البيانات الموجودة مسبقًا. يتم استخدام التعويض لتحسين دقة واكتمال البيانات لتحليلها بشكل صحيح واتخاذ القرارات الناجحة. يعد التعويض عملية مهمة في مجالات مثل بناء نماذج تعلم الآلة وتحليل البيانات والأبحاث العلمية. وهناك العديد من تقنيات التعويض المختلفة التي يمكن استخدامها لتعويض القيم المفقودة بناءً على خصائص البيانات وطبيعة الدراسة. سنتعرف على عدد من هذه التقنيات وستكون على قسمين. تعويض قيمة مفردة او تعويض اكثر من قيمة.

1. مقاييس النزعة المركزية Central Tendency

في هذه الحالة سنقوم بتعويض البيانات باستخدام (Central Value). تستخدم المقاييس التالية في التعرف على هذه القيمة المركزية لتمثيل البيانات:

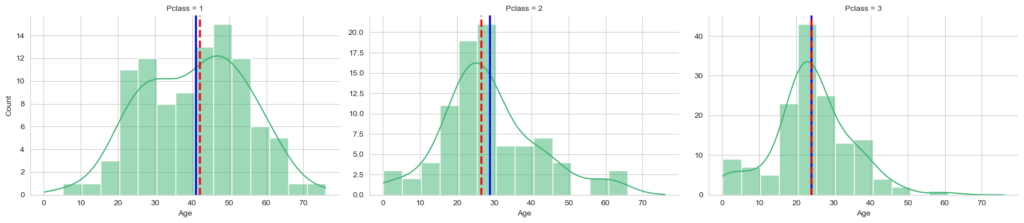
الوسط الحسابي (Mean) : يحصل عليه بقسمة حاصل جمع البيانات على عددها. ويمكن تطبيقها مباشرة على المتغير الذي يحتوي على بيانات مفقودة. ويفضل استخدامة اذا كانت البيانات متوزعة لدينا بشكل طبيعي.

في التوزيع الطبيعي Normal Distribution، تتوزع البيانات بشكل متماثل حول القيمة المتوسطة دون وجود انحراف كبير بين القيم. تتجمع معظم القيم حول منطقة مركزية وتنخفض الاحتمالية لوجود قيم متطرفة كلما ابتعدنا عن المركز.”

الوسيط (Median): وهو القيمة المركزية لمجموعة البيانات. ويتم الحصول عليه بترتيب قيمة البيانات تصاعديًا أو تنازليًا.
إذا كان عدد المتغيرات فرديًا: فيكون الوسيط هو القيمة الوسطى.
إذا كان عدد المتغيرات زوجيًا: فيكون الوسيط هو الوسط الحسابي للقيمتين اللتين في المنتصف.
المنوال (Mode): وهو القيمة الشائعة أو الأكثر تكرارًا بين البيانات أو المشاهدات

سنقوم ببساطة بحساب هذه القيم وتعبئة القيم المفقودة مباشرة. اذا كان لديك اكثر من متغير يحمل نفس عدد التكرار فالافضل الابتعاد عن هذه الطريقة للتعبئة واستبدالها بطريقة اخرى.

بالنسبة للبيانات المنفصلة (Discret)، قد لا يكون Mean دائمًا قيمة صحيحة لأن المتغيرات المنفصلة (Discret) قادرة على اتخاذ قيم محددة ومميزة فقط. لذلك، يُراعى أن يكون Mean الذي تم استخدامه في التعويض قيمة المنفصلة (Discret) صحيحة ضمن نطاق القيم الممكنة لهذا المتغير.

إذا كان للبيانات المنفصلة (Discret) ترتيب طبيعي وأن قيمة Mean هي قيمة صحيحة ضمن هذه المجموعة من القيم المنفصلة (Discret)، فيمكن استخدام تعويض القيم بالمتوسط. على سبيل المثال، إذا كان لديك مجموعة بيانات تمثل عدد المنتجات المباعة (متغير عددي صحيح) وهناك بعض القيم المفقودة، يمكن حساب المتوسط للقيم المتوفرة وتقريبه إلى أقرب قيمة صحيحة للتعويض.

مع ذلك، إذا كانت البيانات المنفصلة (Discret) تمثل فئات أو علامات بدون ترتيب محدد، قد لا يكون تعويض القيم باستخدام Mean هو الخيار المناسب. في مثل هذه الحالات، يُفضل عمومًا النظر في طرق أخرى لتعويض القيم الناقصة، مثل تعويض القيم باستخدام (mode imputation) وهو استخدام القيمة الأكثر تكرارًا، أو استخدام تقنيات النمذجة التنبؤية مثل أقرب جيران (k-NN) .

titanic_central_tendency = titanic_df.copy()
titanic_central_tendency['Age'].fillna(titanic_central_tendency['Age'].mean(), inplace=True)
titanic_central_tendency['Fare'].fillna(titanic_central_tendency['Fare'].median(), inplace=True)
titanic_central_tendency['Cabin'].fillna(titanic_central_tendency['Cabin'].mode()[0], inplace=True)
create_visualization(titanic_central_tendency, 'Imputation using Central Tendency (Mean, Median, Mode)')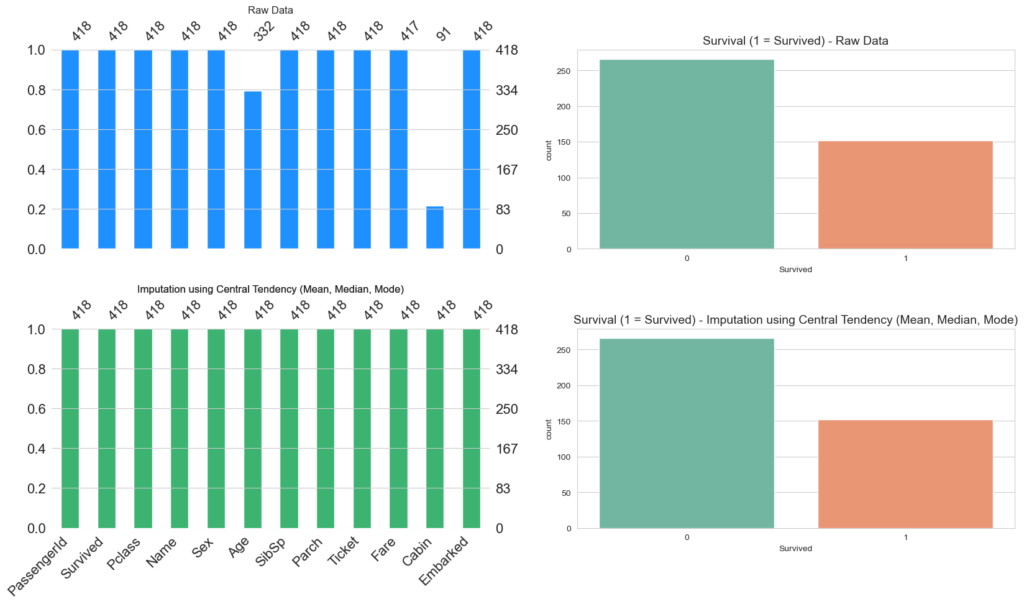

البيانات المنفصلة مقابل البيانات المستمرة:
البيانات المنفصلة هي نوع من البيانات الرقمية التي تتضمن أرقامًا كاملة وملموسة مع قيم بيانات محددة وثابتة يتم تحديدها عن طريق العد مثل عدد المزظفين في قسمك او عدد المنتجات الموجودة في مستودع. تشمل البيانات المستمرة الأرقام المركبة والقيم المتغيرة التي يتم قياسها خلال فترة زمنية معينة مثل درجة الحراره والوزن.

2. البيانات النصية

طبيعي ان يكون لديك بعض البيانات النصية المفقودة في مجموعة البيانات لديك. يمكن حلها باستبدال هذه البيانات بالبيانات الاكثر تكرار في المتغير.

3. التقدير او التنبؤ Prediction

تقدير القيم المفقودة باستخدام البيانات الأخرى في مجموعة البيانات.

الانحدار Regression Imputation

يعتبر الانحدار الخطي أحد أساليب التحليل الإحصائي، ويُستخدم لفهم العلاقة بين متغيرين أو أكثر. في هذه الحالة، نرغب في فهم كيف تتأثر المتغير المستهدف (Y) بمتغيرات توضيحية أخرى (X).

$Y = β₀ + β₁X₁ + β₂X₂ + … + βₙXₙ + ε$

Y هو المتغير المستهدف (المتغير الذي نرغب في التنبؤ به).
X1,X2,…,Xn هي المتغيرات التوضيحية (المتغيرات المستقلة) التي يتم استخدامها للتنبؤ بقيمة Y.
$β_0,β_1,β_2,…,β_n$ هي معاملات (المعاملات) نموذج الانحدار الخطي، والتي تمثل الميل أو التأثير الذي تُمثله كل متغير توضيحي على Y.
ε هو عبارة عن الخطأ، والذي يمثل الفرق بين قيم Y الفعلية وقيم Y المتوقعة بواسطة النموذج. يُعبِّر عن التباين غير المفسر في البيانات.

الخطوة الأولى في عملية تقدير نموذج الانحدار الخطي هي جمع البيانات المتاحة. يتم قياس قيم المتغير المستهدف Y لمجموعة من الحالات، وكذلك قيم المتغيرات التوضيحية X لنفس الحالات. هذه القيم تسمى “القيم المرصودة”.

ثم، يتم استخدام هذه القيم المرصودة لإنشاء النموذج الخطي. يهدف النموذج إلى أن يكون تمثيلاً للعلاقة الخطية بين Y و X. الهدف هو إيجاد خط (معادلة خطية) يمثل العلاقة الأفضل بين المتغيرات.

بعد أن يتم تقدير النموذج، يمكن استخدامه للتنبؤ بالقيم المفقودة لـ Y. يمكننا استخدام النموذج لتوقع القيم المحتملة لـ Y عند تلك القيم لـ X.

توفر هذه الطريقة تقديراً للقيم المفقودة، وتحافظ على العلاقات الخطية بين X و Y، مما يساعد على فهم الارتباطات بين المتغيرات والتنبؤ بقيم المتغير المستهدف بناءً على المتغيرات التوضيحية. على عكس الطرق الأكثر بساطة مثل مقاييس النزعة المركزية، يعتبر الانحدار الخطي أداة قوية للتحليل والتنبؤ في العديد من المجالات البحثية والتطبيقات العملية.

# List of columns to replace 0 with NaN
missing_columns = ["Glucose", "BloodPressure", "SkinThickness", "Insulin", "BMI"]
# Replace 0 with NaN in the specified columns
df[missing_columns] = df[missing_columns].replace(0, np.NaN)
# Show the DataFrame after replacing 0 with NaN
# Define a function for random imputation
def random_imputation(df, feature):
    number_missing = df[feature].isnull().sum()
    observed_values = df.loc[df[feature].notnull(), feature]
    df.loc[df[feature].isnull(), feature + '_imp'] = np.random.choice(observed_values, number_missing, replace=True)
    return df
# Loop through the missing_columns and perform random imputation
for feature in missing_columns:
    df[feature + '_imp'] = df[feature]
    df = random_imputation(df, feature)
# Create a new DataFrame for deterministic imputation results
deter_data = pd.DataFrame(columns=["Det" + name for name in missing_columns])
# Loop through the missing_columns and perform deterministic imputation
for feature in missing_columns:
    deter_data["Det" + feature] = df[feature + "_imp"]
    parameters = list(set(df.columns) - set(missing_columns) - {feature + '_imp'})
    model = LinearRegression()
    model.fit(X=df.loc[df[feature + '_imp'].notnull(), parameters], y=df.loc[df[feature + '_imp'].notnull(), feature + '_imp'])
    deter_data.loc[df[feature].isnull(), "Det" + feature] = model.predict(df.loc[df[feature].isnull(), parameters])
# Show the DataFrame with deterministic imputation results
deter_data.head()
# Visualize missing data patterns for the original DataFrame
msno.matrix(df, color=(0.30, 0.36, 0.44))
# Visualize missing data patterns for the DataFrame with deterministic imputation results
msno.matrix(deter_data, color=(0.30, 0.36, 0.44))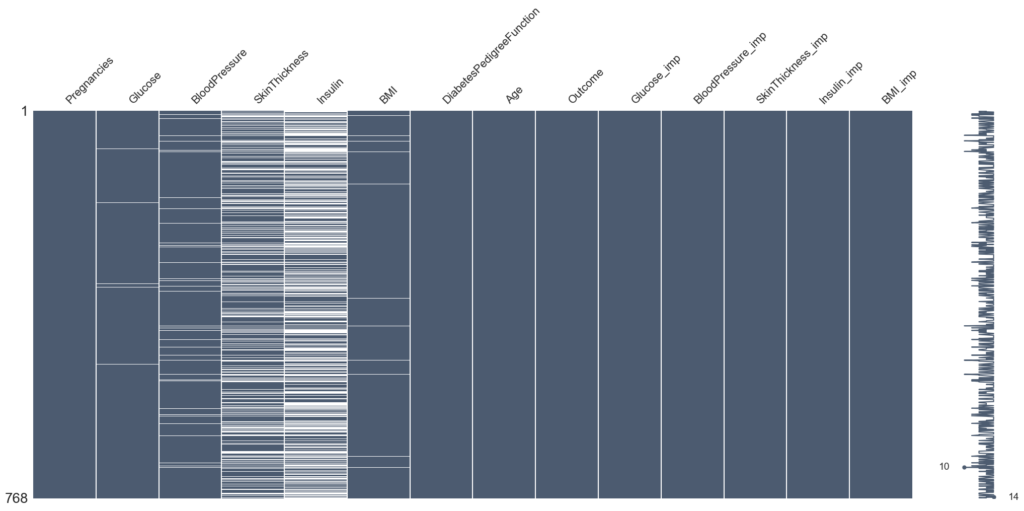

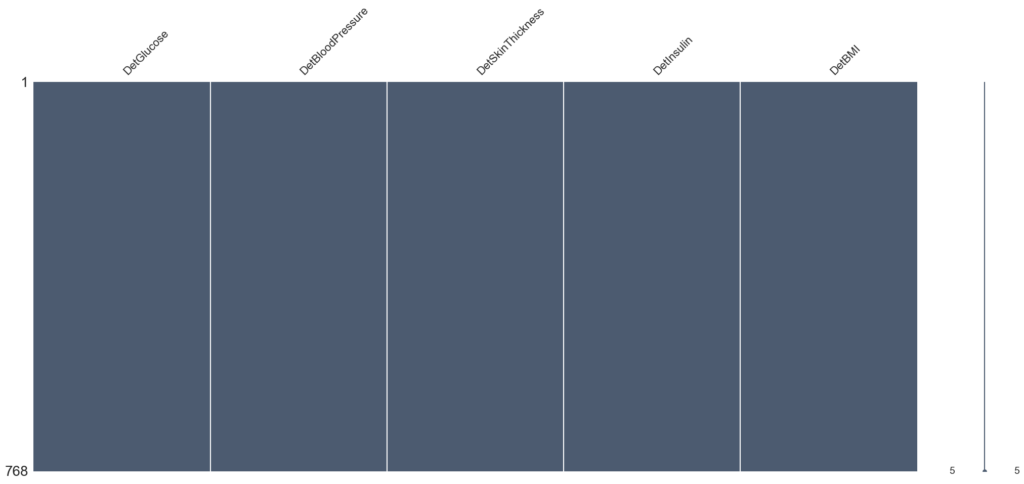
تُعتبر تقنيات التعويض، مثل النزعة المركزية والانحدار، دورًا حيويًا في تحليل البيانات واتخاذ القرارات. من خلال ملء القيم المفقودة بناءً على أنماط البيانات الموجودة، تُعزز هذه الطرق دقة واكتمال مجموعات البيانات، مما يمكِّن من بناء نماذج تعلم ألة دقيقة وايضضًا الحصول علة حقائق اكثر دقة.

خاتمة

في ختام مقالنا، تبين لنا أهمية التعامل مع البيانات المفقودة وتأثيرها على دقة الاستدلال والتحليل. توضح الطرق المذكورة في المقال، مثل حذف البيانات، وتحليل الحالات المتاحة، والتعويض، واستخدام التنبؤ، كيفية التعامل مع هذه البيانات المفقودة وتعويضها بطرق مختلفة ومناسبة للسياق المحدد.

إن اختيار الطريقة المناسبة يعتمد على الطبيعة والهدف من التحليل، فبعض الأوقات قد يكون من الأفضل حذف البيانات المفقودة إذا كانت نسبتها قليلة ولا تؤثر بشكل كبير على النتائج، بينما في حالات أخرى قد يكون من الأفضل استخدام تقنيات التعويض أو التنبؤ لضمان دقة الاستدلال.

على الباحثين والمحللين أن يكونوا حذرين في اختيار الطريقة المناسبة وفهم السياق والبيانات المتاحة جيدًا قبل اتخاذ قراراتهم. تقنيات التعويض والتنبؤ قد تساعد في تحسين جودة البيانات وزيادة دقة النتائج، ولكنها تأتي أيضًا مع تحديات واعتبارات تحتاج إلى النظر فيها.

بالاعتماد على المنهجيات الصحيحة وفهم السياق، يمكن للباحثين والمحللين تحقيق نتائج موثوقة ودقيقة في تحليل البيانات المفقودة، مما يسهم في تطوير فهمنا للظواهر واتخاذ قرارات أفضل استنادًا إلى الأدلة المتاحة.