اليوم بإذن الله سنراجع أهم الأوراق العلمية التي ظهرت غيرت في مفهوم Fine-Tuning نماذج اللغات الضخمة, سأكتب أولاً عن LoRA وبعد ذلك سأقوم بكتابة عن ماذا حدث بعد LoRA.
ليش LoRA؟
عندما نتطلع إلى إعادة ضبط نموذج في مجال الذكاء الاصطناعي، نجد أمامنا تحدٍ كبير ومعروف يتمثل في كمية الموارد المطلوبة لتحديث هذا النموذج. على سبيل المثال، يحتوي نموذج GPT-3 على 175 مليار معلمة! وعندما نرغب في إعادة ضبطه، نجد أنفسنا بحاجة إلى تحميل هذه المعلمات على وحدة معالجة الرسومات GPU، ويمكن تصوّر حجم وموارد النظام اللازمة لتنفيذ هذه العملية. وهذا إذا أردنا القيام بها فقط للاستخدام الفوري كعملية تحليلية.
ومع ذلك، إذا كنا نرغب في تعديل النموذج أو إعادة ضبطه، نحتاج إلى موارد تقريباً مضاعفة، وذلك لأننا نحتاج إلى حفظ أو تحميل مشتقات Gradients لكل معلمة. لماذا؟ لأنه يتعين علينا ضبط الأوزان Weights خلال عملية Backpropagation أثناء التدريب في الشبكات العصبية، وهذا يتم عبر حساب مقدار الفقد Loss الذي تم حسابه سابقاً.
إذاً، يظهر أن العمليات البسيطة لاستخدام النموذج كأداة تحليلية تحتاج إلى موارد هائلة، وعندما نتحدث عن تعديله أو تحسينه، يزيد الضغط على الموارد بشكل كبير، مما يجعل عمليات الضبط تتطلب جهودًا كبيرة ودقة عالية.
مع ظهور ثورة نماذج اللغات الضخمة (LLM)، أصبح هناك اهتمامٌ متزايد بالبحوث والأفكار التي تستهدف إعادة ضبط نماذج اللغات مفتوحة المصدر حتى تكون قابلة للاستخدام على الأجهزة الشخصية. ومن بين هذه الجهود الملحوظة، نجد ما نشرته مايكروسوفت في ورقة علمية حول تقنية LoRA. يُعتبر LoRA أحد الابتكارات البارزة التي ستساهم في إعادة ضبط نماذج اللغات الضخمة باستخدام موارد محدودة أو معقولة.
هذا التحدي لا يقف في مرحلة ضبط النموذج, اذا افترضنا انك قمت بإنجاز المهمة وضبط النموذج ستنتقل حتما الى المرحلة التلية وهي نشره للمستخدمين, عند نشر نموذج بهذا الحجم الهائل يحتاج الى بنية تحتيه عالية الآداء وسريعة في استخراج النتائج, اذا كنت في منظمة متعددة المهام ولديها أكثر من مهمة فحتمًا سيزيد هذا التحدي.
ما ذكر سلفًا من تحديات تعيق عمل المؤسسات الصغيرة والأفراد ويحد من استفادتهم من هذا التطور والنقلة النوعية في مجل الذكاء الاصطناعي, ويكون فقط حكرا على المنظمات الكبيرة ذات الكفاءة العالية, من هنا بدأت الكثير من الحلول والأوراق العلمية في الانتشار في محاولة لضبط هذه النماذج في بيئات بسيطة وتعطي نفس الكفاءة. هذا ما سعت اليه الورقة العلمية LoRA.
تفكيك المصفوفات Matrix decomposition
في الجبر الخطي تفكيك المصفوفة هي عملية رياضية تقوم بتفكيك المصفوفة الى جزئين, الهدف هو تبسيط العمليات الحسابية والتحليلات,فالعمل على أجزاء صغيرة اسهل بكثير من العمل على شيء واحد كبير, غالبًا ما يكون تحليل مصفوفات البيانات، مثل مصفوفات القرب أو الارتباط، صعبًا للغاية ومملًا، لذلك عندما نريد الكشف عن خصائص وبنية المصفوفة، نحتاج إلى تحليل مصفوفة البيانات إلى مصفوفة بيانات أساسية ذات ترتيب أدنى low-order أو رتبة أقل low-rank.

هناك أنواع كثيرة جدًا لتفكيك البيانات ولكن سيكون التركيز فقط على مجزئ القيمة المفردة Singular Value Decomposition وباختصار SDV. هو باختصار كل مصفوفة M∈Cm×n يمكن تفكيكها الى ثلاث مصفوفات *M=UΣV
- U (مصفوفة وحدية m × m): تُمثل هذه المصفوفة القيم الفردية اليسرى. مصفوفة مربعة بأعمدة أورثونورمال، وهذا يعني أن أعمدتها هي نواقص طول 1 ومتعامدة (متعامدة تمامًا) على بعضها البعض.
- Σ (مصفوفة قطرية m × n): تحتوي هذه المصفوفة على القيم الفردية على قطرها وعلى أصفار في باقي الأماكن. القيم الفردية هي قيم غير سالبة. تقدم هذه القيم معلومات حول تكبير وأهمية القيم الفردية المقابلة في مصفوفات U و V*.
- V (مصفوفة وحدية n × n): تُمثل هذه المصفوفة القيم الفردية اليمنى. بشكل مشابه لـ U، مصفوفة مربعة بأعمدة أورثونورمال.
- V* (المتحول المشترك لمتحول V): يُشير المتحول المشترك، الذي يُعرف في كثير من الأحيان بـ V*، إلى المرافق المعقد لناقل V. إذا كانت V مصفوفة حقيقية، فإن V* هي ببساطة نقل V. يُستخدم المتحول المشترك في سياق الأعداد المعقدة لضمان الحفاظ على خصائص التعامل الطولي والأورثونورمالية.
مفاهيم مهمة:
الارتباط الخطي (linear dependence) : مجموعة المتجهات تعتبر تابعة خطياً إذا وفقط إذا كل متجه يمكن كتابته بشكل خطي باستخدام مجموعة من المتجهات الأخرى.
ملاحظة: إذا لم يتحقق هذا الشرط فإنها تسمى مستقلة خطياً .
رتبة المصفوفة (rank): رتبة المصفوفة A يرمز له ب rank(A) وهو يصف حجم الفضاء المتجهي الذي نتج من أعمدة المصفوفة. يمكن وصفه كذلك بأقصى عدد من أعمدة المصفوفة A التي تمتلك خاصية أنها مستقلة خطياً.
النظرية خلف LoRA
الفكرة البسيطة خلف LoRA هو بدلا من تعديل كل الأوزان Weight خلال عملية Fine-Tune, سنقوم بتجميدهم Freez, بمعنى اننا لن نقوم باي اجراء او تعديلات على Weight الأساسية, عوضُا عن ذلك سنقوم بإنشاء Weight منفصل, هذه الأوزان المنفصلة سنقوم بتعديلها بما يتناسب مع المهمة التي نريد ان يقوم بها النموذج, بعد عملية التدريب سنقوم بإضافة هذه الأوزان الى النموذج الأساسي ومن ثم سنقوم باستخدام النموذج الأساسي مع الأوزان المعدلة للقيام بعمليات Infrence للمهمة المطلوبة منه.
عندما نريد استخدام النموذج في عمليات الـinfernce سنقوم بتحميل الأوزان في GPU دون الحاجة الى زيادة سعة الذاكرة لأننا قمنا بعملية إضافة لأوزان النموذج الأساسي مضافُا له النموذج المعدل, وهذا يعني انه اصبح لدينا فقط وزن واحد خاص بالنموذج وليس وزنين كما كان يحدث سابقُا.

الفكرة التي طرحتها الورقة العلمية ان النماذج المُدربة سابقًا والتي تحتوي على عدد كبير من المعلمات هي في الحقيقة يمكن ان تكون ذات بُعد أقل. وأن التغيرات في الوزن الناتجة عن الانحدار التدريجي (gradient descent) تكون لها رتبة داخلية أقل. فبدلًا من التعامل مع جميع المعلمات يمكن تبسيطها في بعد أقل, المُقترح هو تمثيلها في أبعاد أقل باستخدام مجزئ القيمة المفردة (Singular Value Decomposition أو SVD)، ثم القيام بانحدار تدريجي (gradient descent) لتحسين الأوزان في هذه الأبعاد الأقل. الهدف هو تقليل التعقيد الحسابي وتحسين كفاءة التدريب للنماذج ذات العدد الكبير من المعلمات.
البنية الخاصة بـLoRA
الآن وبعد اتضاح الصورة الكبيرة لطريقة عمل LoRA, ما لذي اضافوه بالتحديد حتى يعطينا هذه النتائج, الآن سنلقي نظرة على الصورة الموجودة في الورقة العلمية ونناقش بعض من جوانبها

تلاحظ وجود جزئين:
- الجزء الأزرق: هي المعاملات بشكل كامل dxd, أي انها بكامل ابعادها, هذا الجزء هو key,value و query.
- الجزء البرتقالي: هي الفكرة نلاحظ وجود مصفوفتين:
- B : تم إعطائها قيمة مبدئية بـ0 وبعادها هي dXr
- A: تم تهيئتها بـGaussian ومتوسط 0 وأيضا الانحراف المعياري وبعادها تكون rxd.
الآن الصورة شبه واضحة وهذا يعكس المعادلة التالية
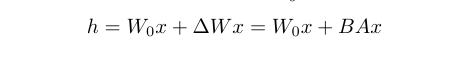
- W0: هو الوزن
- x : البيانات المدخلة
- deltaWx : هو الانحدار (gradient) والتي يمكن تمثيلها بـBA ذات الابعاد الأقل.
الفوائد
حققت التقنيات المحسّنة في التجربة من استخدام أكثر فعالية للذاكرة، وتقليل متطلبات التخزين، وتسريع أوقات التدريب، وزيادة المرونة لنشر والتبديل بين المهام المختلفة.
- تقليل في استهلاك الذاكرة والتخزين:
- الميزة الرئيسية هي التقليل الكبير في استهلاك الذاكرة العشوائية (RAM) ومساحة التخزين.
- عند تقليل بُعد النموذج (d_{\text{model}}) يتم تقليل استخدام الذاكرة العشوائية بنسبة تصل إلى ثلثيها.
- على سبيل المثال، في حالة تدريب نموذج ترانسفورمر كبير باستخدام محسن Adam، يتم تقليل استهلاك VRAM أثناء التدريب لـ GPT-3 175B من 1.2 تيرابايت إلى 350 جيجابايت.
- تحسين للمعلمات المجمدة Frozen Parameters:
- تتضمن استراتيجية التحسين عدم تخزين حالات المحسن للمعلمات المجمدة، وهو ما يسهم في تقليل استخدام VRAM.
- تقليل حجم نقطة الفحص Checkpoint:
- باستخدام عامل التقليل (
r) البالغ 4 وتكييف مصفوفات الاستعلام والقيم فقط، يتم تقليل حجم نقطة الفحص checkpoints بشكل كبير. - يتم تقليل الحجم بنحو 10,000 مرة، من 350 جيجابايت إلى 35 ميجابايت.
- باستخدام عامل التقليل (
- فاعلية في التدريب:
- يتيح حجم نقطة الفحص checkpoint المقلل التدريب بفعالية أكبر باستخدام عدد أقل من وحدات المعالجة الرسومية GPU، مما يقلل من حدوث I/O.
- تُعزز القدرة على التبديل بين المهام أثناء النشر بتكلفة أقل من خلال استبدال وزن LoRA فقط بدلاً من جميع المعلمات.
- تحسين في الأداء:
- يُلاحظ تسريع بنسبة 25% أثناء التدريب على GPT-3 175B مقارنة بالضبط الكامل.
- يرجع ذلك إلى عدم الحاجة إلى حساب التدرجات Gradiant لمعظم المعلمات.
كيف يمكن تحديد افضل رتبة Rank
ربما بدر الى ذهنك كيف اعرف افضل رتبة! هذا التساؤل أيضا كان لدى الباحثين وهنا سنقوم بإضافة بعض الجداول من الورقة العلمية وشرحها.
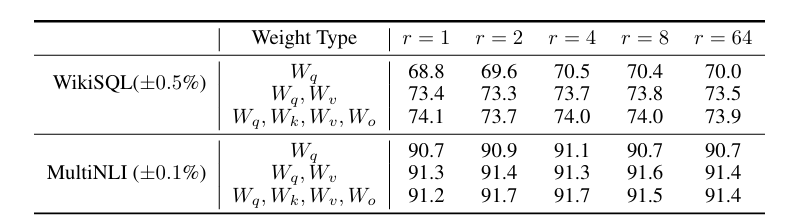
من الجدول نلاحظ ان الرتبة الصغيرة (r) تتكيف بشكل فعال مع تمثيلات (Wq) والقيمة (Wv) في مجموعات بيانات WikiSQL وMultiNLI. والجدير بالذكر أن أداء LoRA تعطي نتائج ممتازة مع r صغير جدًا، مما يعني أن مصفوفة التحديث ∆W قد يكون لها “رتبة جوهرية” صغيرة. يشير هذا إلى أن مصفوفة التكيف ذات الرتبة المنخفضة كافية، حيث أن زيادة r لا يبدو أنها تلتقط مساحة فرعية أكثر أهمية.
ما هي مصفوفات الوزن WEIGHT MATRICES في المحولات TRANSFORMER التي يجب أن نطبق عليها LORA؟
أي فئات من الأوزان يجب علينا تكييفها باستخدام LoRA لتحقيق أفضل أداء في المهام؟
نطبق LoRA على self-attention , نحدد معلمة 18 مليون (تقريباً 35 ميجابايت عند التخزين بتنسيق FP16) لنموذج GPT-3 بحجم 175 مليار، وهذا يتوافق مع r = 8 إذا تم تكييف نوع واحد من أوزان الانتباه أو r = 4 إذا تم تكييف نوعين، عبر جميع الطبقات البالغ عددها 96, كانت النتائج كما في الجدول
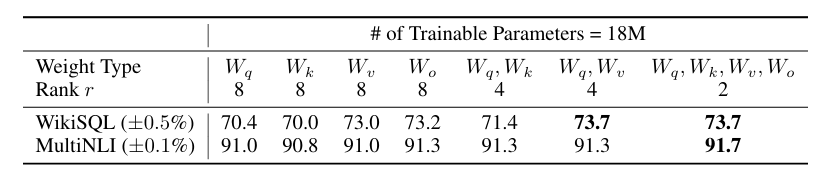
تقييم دقة التحقق على مجموعات البيانات WikiSQL و MultiNLI بعد تطبيق LoRA على أنواع مختلفة من أوزان الانتباه (attention weights) في GPT-3، مع الحفاظ على نفس عدد المعلمات القابلة للتدريب. يظهر بشكل لافت أن تحقيق أفضل أداء عام يحدث عند تكييف كل من Wq و Wv. يظل انحراف المعيار ثابتًا عبر Random Seeds المختلفة لكل مجموعة بيانات، كما هو موضح في العمود الأول. يجدر بالذكر أن وضع جميع المعلمات في Wq أو Wk يؤدي إلى أداء أقل بشكل كبير، بينما يعطي تكييف كل من Wq و Wv أفضل نتيجة. يشير هذا إلى أنه حتى مع الرتبة Rank يبلغ أربعة، يتم التقاط معلومات كافية في W بحيث يكون من المفضل تكييف مصفوفات أوزان أكثر بدلاً من تكييف نوع واحد من الأوزان برتبة أكبر.
الخلاصة
قدمت LoRA تقنية جديدة لإعادة تطويع النماذج الضخمة لمهام جديدة, بتفكيك المعلمات الضخمة الى أجزاء ذات بعد اقل يمكن التعامل معها بشكل سريع, أيضا قللت الموارد المطلوبة لحفظ نقاط التحقق للنماذج وتعديلها, الفكرة المطروحة في الورقة العلمية كانت اسهل مما تتخيل واعطت نتائج مقاربة لتعديل النماذج ببعدها الكامل.
المصادر
LORA: LOW-RANK ADAPTATION OF LARGE LAN GUAGE MODEL







